Galaxy Catalog Analysis Example: Galaxy-galaxy lensing¶
In this example, we’ll show how to calculate \(\Delta\Sigma(r),\) the galaxy-galaxy lensing signal of a mock catalog.
There is also a Jupyter Notebook in the following location that can be used as a companion to the material in this section of the tutorial:
halotools/docs/notebooks/galcat_analysis/basic_examples/galaxy_catalog_analysis_tutorial3.ipynb
By following this tutorial together with this notebook, you can play around with your own variations of the calculation as you learn the basic syntax.
Generate a mock galaxy catalog¶
Let’s start out by generating a mock galaxy catalog into an N-body simulation in the usual way. Here we’ll assume you have the z=0 rockstar halos for the bolshoi simulation, as this is the default halo catalog.
from halotools.empirical_models import PrebuiltSubhaloModelFactory
model = PrebuiltSubhaloModelFactory('behroozi10')
from halotools.sim_manager import CachedHaloCatalog
halocat = CachedHaloCatalog(simname = 'bolshoi', redshift = 0, halo_finder = 'rockstar')
model.populate_mock(halocat)
Extract subsamples of galaxies and dark matter particles¶
Predictions for galaxy-galaxy lensing are calculated from the
cross-correlation between the galaxy positions and the dark matter
density field. For the latter, we will use the dark patter particle
positions stored in the ptcl_table attribute of the mock.
px = model.mock.ptcl_table['x']
py = model.mock.ptcl_table['y']
pz = model.mock.ptcl_table['z']
As described in Formatting your xyz coordinates for Mock Observables calculations,
functions in the mock_observables package
such as delta_sigma take array inputs in a
specific form: a (Npts, 3)-shape Numpy array. You can use the
return_xyz_formatted_array convenience
function for this purpose, which has a built-in mask feature
that we’ll also demonstrate to select a random downsampling of \(10^{5}\)
dark matter particles.
px = model.mock.ptcl_table['x']
py = model.mock.ptcl_table['y']
pz = model.mock.ptcl_table['z']
from halotools.mock_observables import return_xyz_formatted_array
import numpy as np
Nptcls_to_keep = int(1e5)
randomizer = np.random.random(len(model.mock.ptcl_table))
sorted_randoms = np.sort(randomizer)
ptcl_mask = np.where(sorted_randoms < sorted_randoms[Nptcls_to_keep])[0]
particle_positions = return_xyz_formatted_array(px, py, pz, mask = ptcl_mask)
Now we’ll extract the x, y, z positions of various subsamples of our galaxies.
x = model.mock.galaxy_table['x']
y = model.mock.galaxy_table['y']
z = model.mock.galaxy_table['z']
mstar11_mask = model.mock.galaxy_table['stellar_mass'] > 1e11
mstar11_positions = return_xyz_formatted_array(x, y, z, mask = mstar11_mask)
mstar105_mask = (model.mock.galaxy_table['stellar_mass'] > 10**10.3) & (model.mock.galaxy_table['stellar_mass'] < 10**10.7)
mstar105_positions = return_xyz_formatted_array(x, y, z, mask = mstar105_mask)
mstar105_central_mask = mstar105_mask * (model.mock.galaxy_table['halo_upid'] == -1)
mstar105_central_positions = return_xyz_formatted_array(x, y, z, mask = mstar105_central_mask)
mstar105_satellite_mask = mstar105_mask * (model.mock.galaxy_table['halo_upid'] != -1)
mstar105_satellite_positions = return_xyz_formatted_array(x, y, z, mask = mstar105_satellite_mask)
Calculate \(\Delta\Sigma(R_{\rm p})\)¶
As of Halotools 0.5, the delta_sigma function requires you to
specify the particle masses of your simulation, as well as the factory by which you have
randomly downsampled the particles in the snapshot to perform your calculation.
logrp_bins = np.linspace(-1,1,15)
rp_bins = 10**logrp_bins
particle_masses = halocat.particle_mass
period=model.mock.Lbox
downsampling_factor = (halocat.num_ptcl_per_dim**3)/float(len(particle_positions))
effective_particle_masses = particle_masses*downsampling_factor
result_mstar11_in_mpc = mean_delta_sigma(mstar11_positions, particle_positions,
effective_particle_masses,
rp_bins, period)
result_mstar105_in_mpc = mean_delta_sigma(mstar105_positions, particle_positions,
effective_particle_masses,
rp_bins, period)
result_mstar105_central_in_mpc = mean_delta_sigma(mstar105_central_positions, particle_positions,
effective_particle_masses,
rp_bins, period)
result_mstar105_satellite_in_mpc = mean_delta_sigma(mstar105_satellite_positions, particle_positions,
effective_particle_masses,
rp_bins, period)
Recall that all Halotools length units are comoving and in Mpc/h. However, the conventional units to plot \(\Delta\Sigma\) are \(h*M_{\odot}/pc^2\), since in those units the galaxy-galaxy lensing signal is roughly order unity for typical \(L_{\ast}\) galaxy samples. So now we convert units and plot the results.
length_unit_conversion = 1e6
result_mstar11_in_pc = result_mstar11_in_mpc/length_unit_conversion**2
result_mstar105_in_pc = result_mstar105_in_mpc/length_unit_conversion**2
result_mstar105_satellite_in_pc = result_mstar105_satellite_in_mpc/length_unit_conversion**2
result_mstar105_central_in_pc = result_mstar105_central_in_mpc/length_unit_conversion**2
Plot the results¶
logrp_mids = 0.5*(logrp_bins[:-1] + logrp_bins[1:])
fig, ax = plt.subplots(1, 1, figsize=(8, 6))
__=plt.loglog()
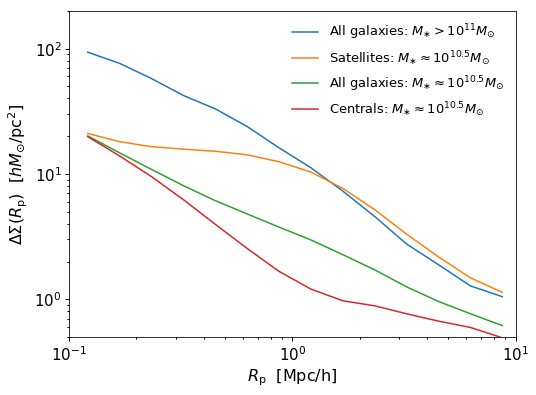
__=ax.plot(10**logrp_mids, result_mstar11_in_pc, label=r'All galaxies: $M_{\ast} > 10^{11}M_{\odot}$')
__=ax.plot(10**logrp_mids, result_mstar105_satellite_in_pc, label=r'Satellites: $M_{\ast} \approx 10^{10.5}M_{\odot}$')
__=ax.plot(10**logrp_mids, result_mstar105_in_pc, label=r'All galaxies: $M_{\ast} \approx 10^{10.5}M_{\odot}$')
__=ax.plot(10**logrp_mids, result_mstar105_central_in_pc, label=r'Centrals: $M_{\ast} \approx 10^{10.5}M_{\odot}$')
__=ax.set_xlim(0.1, 10)
__=ax.set_ylim(0.5, 200)
__=ax.set_xlabel(r'$R_{\rm p} $ $\rm{[Mpc / h]}$', fontsize=16)
__=ax.set_ylabel(r'$\Delta\Sigma(R_{\rm p})$ $[h M_{\odot} / {\rm pc}^2]$', fontsize=16)
__=ax.legend(loc='best', fontsize=13)
This tutorial continues with Galaxy Catalog Analysis Example: Projected galaxy clustering.