monte_carlo_from_cdf_lookup

halotools.utils.monte_carlo_from_cdf_lookup(x_table, y_table, mc_input='random', num_draws=None, seed=None)

Randomly draw a set of num_draws points from any arbitrary input distribution function. The input distribution is specified in terms of its CDF, which is defined by the values of the input y_table of the CDF evaluated at an input set of control points x_table. The input x_table and y_table can be calculated from any input dataset using the function build_cdf_lookup.

Parameters:

x_tablendarray

Numpy array of shape (npts, ) providing the control points at which the input CDF has been tabulated.

y_tablendarray

Numpy array of shape (npts, ) providing the values of the random variable associated with each input control point.

mc_inputndarray, optional

Input array of shape (num_desired_draws, ) storing values between 0 and 1 specifying the values of the CDF for which associated values of y are desired. If mc_input is left unspecified, the num_draws must be specified; in this case, the CDF will be randomly sampled.

num_drawsint, optional

Desired number of random draws from the input CDF. num_draws must be specified if mc_input is left unspecified.

seedint, optional

Random number seed used in the Monte Carlo realization.

Returns:

mc_realizationndarray

Length-num_draws array of random draws from the input CDF.

Notes

See the Transformation of Probability tutorial for pedagogical derivations associated with inverse transformation sampling.

Examples

In this first example, we’ll start by creating some fake data, y, drawn from a weighted combination of a Gaussian and a power law. We’ll think of the fake data y as if it came from some external dataset that we want to model, treating the fake data as our input distribution. We will use the build_cdf_lookup function to build the necessary lookup tables x_table and y_table, and then use the monte_carlo_from_cdf_lookup function to generate a Monte Carlo realization of the data y.

>>> npts = int(1e4)
>>> y = 0.1*np.random.normal(size=npts) + 0.9*np.random.power(2, size=npts)
>>> x_table, y_table = build_cdf_lookup(y)
>>> result = monte_carlo_from_cdf_lookup(x_table, y_table, num_draws=5000)

The returned array result is a stochastic Monte Carlo realization of the distribution specified by y.

Now let’s consider a second example where, rather than specifying an integer number of purely random Monte Carlo draws, instead we pass in an array of uniform random numbers.

>>> uniform_randoms = np.random.rand(npts)
>>> result2 = monte_carlo_from_cdf_lookup(x_table, y_table, mc_input=uniform_randoms)

This alternative call to monte_carlo_from_cdf_lookup provides completely equivalent results as the first, because we have passed in uniform randoms. Since uniform_randoms just stores random values, then random values from the input distribution will be returned.

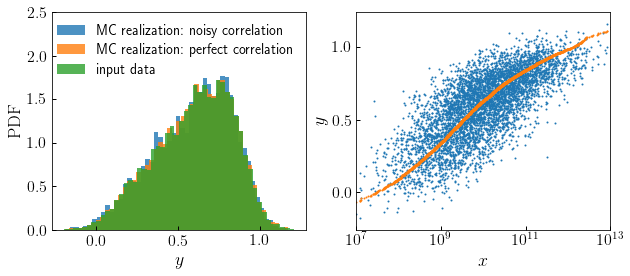
However, this alternative form of input can be exploited for other applications. Suppose that instead of purely random draws, you wish to draw from the input distribution y in such a way that you introduce a correlation between the drawn values and the values stored in some other array, x. You can accomplish this by passing in the rank-order percentile values of x instead of uniform randoms. This is the basis of the conditional abundance matching technique implemented by the conditional_abunmatch_bin_based function.

To see an example of how this works, let’s create some fake data for some property x that we wish to model as being correlated with Monte Carlo realizations of y while preserving the PDF of the realization:

>>> x = np.sort(10**np.random.normal(loc=10, size=5000))
>>> x_percentile = (1. + np.arange(len(x)))/float(len(x)+1)
>>> correlated_result = monte_carlo_from_cdf_lookup(x_table, y_table, mc_input=x_percentile)
>>> uniform_randoms = np.random.rand(npts)
>>> uncorrelated_result = monte_carlo_from_cdf_lookup(x_table, y_table, mc_input=uniform_randoms)

We can use the noisy_percentile to introduce variable levels of noise in the correlation.

>>> from halotools.empirical_models import noisy_percentile
>>> noisy_x_percentile = noisy_percentile(x_percentile, correlation_coeff=0.75)
>>> weakly_correlated_result = monte_carlo_from_cdf_lookup(x_table, y_table, mc_input=noisy_x_percentile)